微分方程模型#
😊一些latex代码在第一次加载不会解析,按f5刷新后可见
人口模型#
在人口模型中,马尔萨斯模型(Malthusian Model)和Logistic模型是两种常见的人口增长模型,它们具有以下特点:
- 马尔萨斯模型:
马尔萨斯模型是由英国经济学家托马斯·罗伯特·马尔萨斯(Thomas Robert Malthus)提出的,用于描述人口增长的指数爆发趋势。该模型基于以下假设:人口具有指数增长的趋势,而资源的增长速度相对较慢,导致人口与资源之间的不平衡。马尔萨斯模型认为,人口增长受到生育率的正向影响和资源限制的负向影响。当人口超过资源承载能力时,会发生人口崩溃或调整。 - Logistic模型:
Logistic模型是基于马尔萨斯模型的扩展,考虑到资源的有限性和生态系统的稳定性。该模型认为,人口增长不会一直保持指数增长,而是在达到一定阈值后逐渐趋于饱和。Logistic模型引入了饱和增长因素,通常使用S形曲线来描述人口增长的趋势。初始阶段,人口增长较快,但随着人口数量的增加,资源的压力逐渐增大,人口增长率逐渐减缓,最终趋于稳定。
马尔萨斯模型和Logistic模型在人口增长的描述和预测上有所不同。马尔萨斯模型强调指数爆发式的人口增长趋势,着重分析人口和资源之间的关系,警示人口过快增长可能引发的问题。而Logistic模型则更加接近实际情况,考虑了资源的有限性,认为人口增长会受到资源限制的影响,逐渐趋于稳定。Logistic模型更符合实际观测到的人口增长趋势,可以更准确地预测人口的未来发展。
1. Malthus(马尔萨斯人口模型)#
变量表示:
- (t, P(t)):表示人口的数对,t为时间,P(t) 为 t 时刻的人口数
-
b, p:分别表示出生率、死亡率
比如说,2002年年初人口总数是 p ,则2002年出生的人数和死亡的人数就分别是 bp 和 dp . 所以,2003年年初的人口总数是
\(p + bp -dp = (1 + b + d) p = (1 + r)p\)
-
这里的 r 是自然增长率。该模型是离散的,但是人口数很大,人口变化(人的生死)是在短时间内随时在发生,故可以看成是连续模型。
-
类似于瞬时速度,t 时刻的人口增长率,为人口平均增长率在所用时间趋于 0 时的极限:
\(r(t) = lim_{▵t\rightarrow0}\frac{P(t+▵t)-P(t)}{▵t}\)
假设:
- 人口发展过程比较平稳;
- 人口数量为时间的连续可微函数;
- 人口增长率是与时间无关的常数 ;
由前面的分析可得
\(P(t+▵t)-P(t)=rP(t)▵t\)
$P(t+dt)-P(t)=rP(t)dt$ (离散形式)
$\frac{dP(t)}{dt}=rP(t)$ , $P(t_0)=P_0$ (连续形式)
进一步得到 Malthus 人口模型
$P(t)=P_0e^{r(t-t_0)}$
MATLAB代码求解#
syms r P(t) t0 P0
eqn=diff(P,t)==r*P;
cond=P(t0)==P0;
PSol(t)=dsolve(eqn, cond); % 返回符号函数symfun
simplify(PSol(t))
运行结果:
ans=P0*exp(r*(t - t0))
2 . Logistic人口模型#
-
阻滞增长模型
Malthus人口模型假设人口增长率 r 为常数,导致了人口指数增长到无穷,这是不合理的。因为没有考虑到有限的资源对种群的增长会产生遏制作用。
假设
- 人口增长率是人口数量的递减函数;
- 确定的环境内的资源供给为常数,且对每个个体的分配是均等的。这表明:当人口规模(密度)增大时,每个人食物的平均分配量必然减少,从而导致人口增长率降低。
-
(对人口增长率做修正):让它不再是常数 r,而是时间 t 的函数 ,让它通过 t 时刻人口数量来起作用,假设是这样作用:
\(r(t)=r(P(t))=r(1-\frac{P(t)}{K})\)
这里 K 为新引入的参数,表示地球所能容纳的最大人口数量。
Malthus 时代, P(t) 相对于 K 来说很小,括号项很接近1,所以也就合理了。若取 K=+∞,就退化为 Malthus 人口模型。
用 N(t) 表示 t 时刻的人口数,类似 Malthus 人口模型,可得到 Logistic 人口模型:
$\frac{dN(t)}{dt}=r(1-\frac{N(t)}{K})$
$N(t_0)=N_0$
仍用分离变量法就能求解:\(N(t)=\frac{k}{1+Ce^{-r(t-t_0)}}\)
其中 C=\(\frac{K-N_0}{N_0}\)
MATLAB代码求解#
syms r K N(t) t0 N0
eqn = diff(N,t) == r * (1 - N/K) * N;
cond = N(t0) == N0;
NSol(t) = dsolve(eqn, cond) % 返回符号函数symfun
simplify(NSol(t))
运行结果:
Nsol(t) = K/(exp(K*((log(K/N0-1) + r*t0)/K – (r*t)/K)) + 1)
ans =(K*N0*exp(r*(t – t0)))/(K - N0 + N0*exp(r*(t - t0)))
考察时间 t 趋近于无穷大时的极限,可以发现结果与 Malthus 模型完全不同!
具体做法:
1.先粗略(目测)估计一个$\psi$ ,它是容纳量的界限,拐点处是它的一半,
有了它再对$\frac{N(t)}{\psi}$ 做 Logit 变换。
2) 再用线性回归估计系数 \(\psi_2\),\(\psi_3\),这样就得到了要估计的3个参数较好的一组初始值。
3) 有了这 3 个参数的较好的初始值,再做原模型的非线性拟合。
3 . Leslie 人口模型#
只对人口总量建模是不够的,特别是需要研究和年龄段有关的问题:老龄化、劳动力人口等。这就需要关注人口的年龄分布(每个年龄段人口的数量),适合的数学模型是基于差分方程理论的Leslie模型。
Leslie模型,是基于年龄和性别,将人口各年龄段的发展过程建立差分方程组,引入矩阵表示后可变成离散矩阵模型。**Leslie模型构建的基本原理**:首先将人口按性别分组,针对女性人口,选择某初始时期,记分年龄段的女性人口数作为一个列向量;然后通过各年龄段生育率、存活率构建 Leslie 人口矩阵;接着,用Leslie人口矩阵左乘分年龄段的女性人口向量,得到新的列向量即为预测的下一阶段分年龄段的女性人口向量;最后,根据男女性别比例推算出人口总数,根据预测年龄分布可以计算平均年龄、平均寿命、老龄化指数、抚养指数等。
对女性人口按年龄切分,记为按年龄段的女性人口向量:
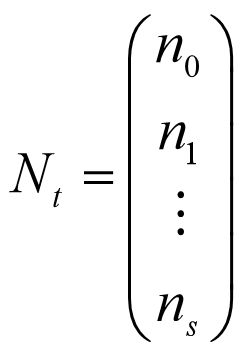
例如,0~4岁用 \(n_0\)表示,5~9岁用\(n_1\)表示,……,85-89岁用\(n_{s-1}\) 表示,90岁及以上用 \(n_s\)表示,各年龄段女性人口的转移关系如下:
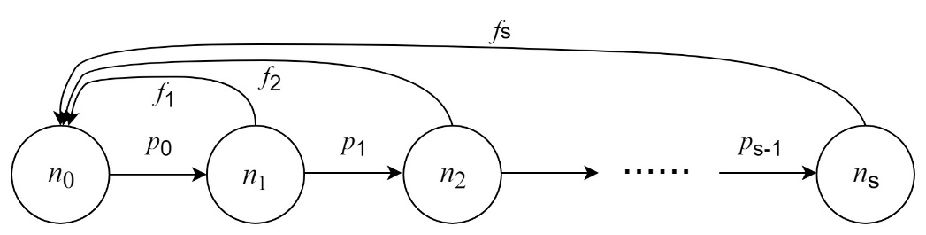
各年龄段女性人口的转移关系图
传染病模型#
这里是对指数传播模型、SI模型、SIS模型和SIR模型的简要介绍及其各自的特点:
- 指数传播模型:
指数传播模型是一种简化的传染病传播模型,假设传染病在人群中以指数增长的方式传播。该模型基于以下假设:每个感染个体在一定时间内以固定的概率将疾病传播给其他人,感染个体不会康复或移除。这种模型适用于早期传染病的快速传播阶段,但不适用于描述疾病的自然消退或人群免疫的情况。 - SI模型:
SI模型是一种基本的传染病传播模型,其中S表示易感者(Susceptible)和I表示感染者(Infected)。该模型假设人群中没有免疫力,感染者不会康复或移除。SI模型适用于描述传染病的初始传播阶段,但不考虑康复或移除的情况。 - SIS模型:
SIS模型是一种常见的传染病传播模型,其中S表示易感者(Susceptible)、I表示感染者(Infected)和R表示康复者(Recovered)。该模型假设感染者可以康复并重新变为易感者,而没有获得持久免疫力。SIS模型适用于描述某些传染病,如感冒或性传播疾病,其中个体可以反复感染。 - SIR模型:
SIR模型是一种常用的传染病传播模型,其中S表示易感者(Susceptible)、I表示感染者(Infected)和R表示康复者(Recovered)。该模型假设感染者经过一定的传染期后可以康复并获得持久免疫力,不再感染该病。SIR模型适用于描述具有持久免疫力的传染病,如麻疹或风疹。 - SEIR模型:
SEIR模型是一种常用的流行病学模型,用于描述传染病在人群中的传播过程。SEIR模型将人群分为四个主要的舱室:易感者(Susceptible)、潜伏者(Exposed)、感染者(Infectious)和康复者(Recovered)。
下面是对SEIR模型中每个舱室的含义和转换过程的解释:
- 易感者(Susceptible):这个舱室包括尚未感染病原体的个体,但他们对病原体具有易感性,可以被感染。
- 潜伏者(Exposed):这个舱室包括已经感染病原体但尚未表现出明显症状的个体。潜伏期是指从感染病原体到出现临床症状的时间间隔。在潜伏期内,个体可以传播病原体给其他人,尽管他们自己没有明显的症状。
- 感染者(Infectious):这个舱室包括已经感染病原体且能够传播给其他易感者的个体。感染者通常表现出明显的症状,如发热、咳嗽等。
- 康复者(Recovered):这个舱室包括已经康复并具有免疫力的个体。康复者在经历感染后,可以恢复健康并获得对病原体的免疫力,从而不再易感。
在SEIR模型中,个体之间的转换过程可以用一组微分方程来描述。这些方程考虑了人群中个体之间的接触、感染、潜伏和康复的过程,以及相应的参数,如传染率、潜伏期和康复率等。通过解析这些方程,可以模拟和预测传染病在人群中的传播动态,帮助评估不同防控策略的效果。
SEIR模型是一种相对较复杂的流行病学模型,适用于描述具有潜伏期的传染病,如流感、麻疹等。它提供了更详细的传染病传播过程的描述,有助于理解和预测疫情的发展趋势,并为制定公共卫生干预措施提供科学依据。
这些模型在传染病传播的过程中考虑了不同的因素和假设,可以用于分析传染病的传播动态、预测疫情趋势以及评估不同的防控策略。需要注意的是,这些模型是简化的理论框架,实际应用中可能需要根据具体情况进行适当的调整和扩展。